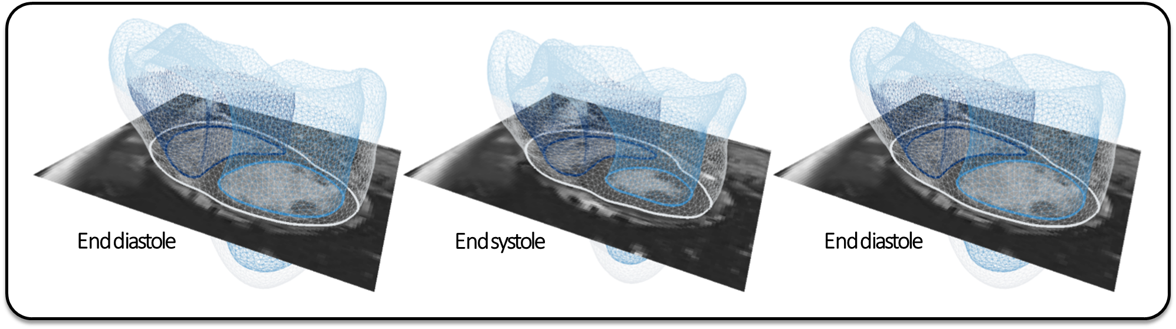
Cardiac motion tracking on cine MRI data. The data is a time series of images. The aim is to recover the motion of the cardiac muscle over time.
Cardiac motion tracking on cine MRI data. The data is a time series of images. The aim is to recover the motion of the cardiac muscle over time.
We extend Bayesian models of non-rigid image registration to allow not only for the automatic determination of registration parameters (such as the trade-off between image similarity and regularization functionals), but also for a data-driven, multiscale, spatially adaptive parametrization of deformations. Adaptive parametrizations have been used with success to promote both the regularity and accuracy of registration schemes, but so far on non probabilistic grounds – either as part of multiscale heuristics, or on the basis of sparse optimization. Under the proposed model, a sparsity-inducing prior on transformation parameters complements the classical smoothness-inducing prior, and favors parametrizations that use few degrees of freedom. As a result, finer bases get introduced only in the presence of coherent image information and motion, while coarser bases ensure better extrapolation of the motion to textureless, uninformative regions. The space of possible parametrizations consists of arbitrary combinations of basis functions chosen among any preset, widely overcomplete (and typically multiscale) dictionary. Inference is tackled in an efficient Variational Bayes framework. In addition we propose a flexible mixture-of-Gaussian model of data that proves to be more faithful for a variety of image modalities than the sum-of-squared differences. The performance of the proposed approach is demonstrated on time series of (cine and tagged) magnetic resonance and echocardiographic cardiac images. The proposed algorithm matches the state-of-the-art on benchmark datasets evaluating accuracy of motion and strain, and is highly automated.