Selected Publications

Medical image registration takes a pair of images and returns a transformation of space that captures the underlying non rigid motion, so that images are correctly 'aligned'. This is challenging because of changing organ appearance, random imaging artefacts, because 3D volumes are large, and because many transformations could possibly yield the same observed motion. Intuitively, we'd like to find a smooth solution, whose mathematical representation is multiscale and just complex enough to capture the observed motion - no more, no less. We introduce a probabilistic formulation of registration that does just that. The back-end is an efficient algorithm for structured sparse Bayesian inference.
In MedIA, Feb 2017
Details PDF Slides Project

Projects

Bayesian Medical Image Registration

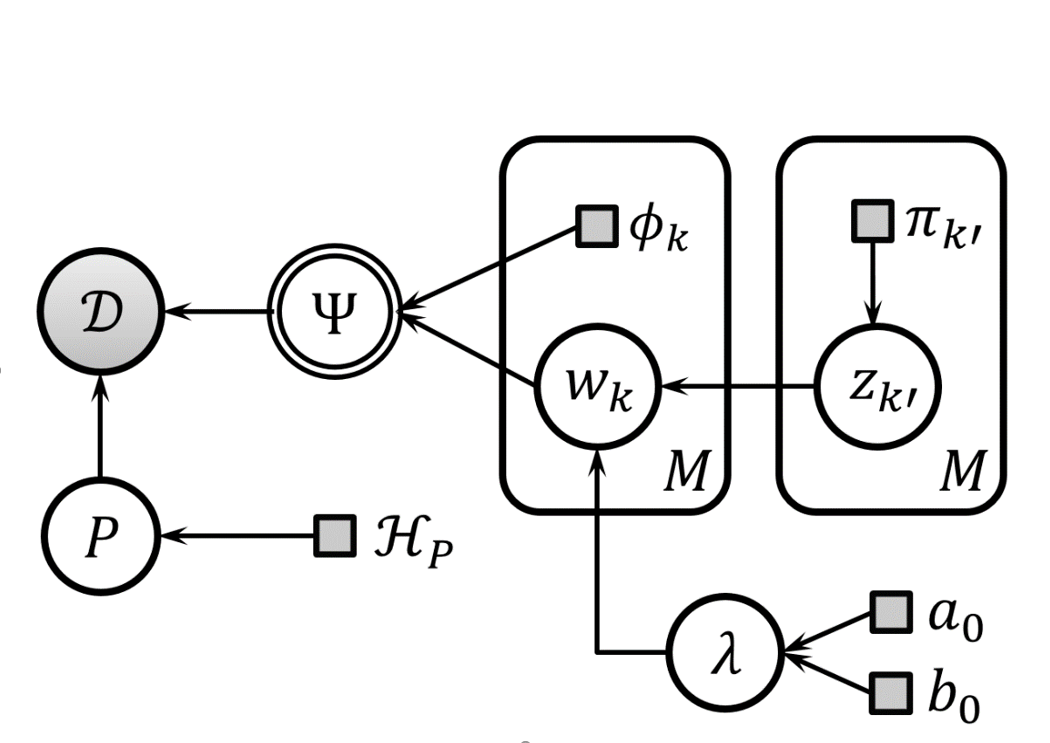
Non-rigid registration schemes supplement incomplete observations (image data) with prior assumptions (e.g. plausible object deformations, image formation). They operate under data noise, model biases and uncertainties. The ability to quantify those uncertainties and to analyze the soundness of model assumptions is very appealing, especially if registration is part of a larger pipeline. The project aims at a fully Bayesian treatment of registration, as a natural framework to address these questions.

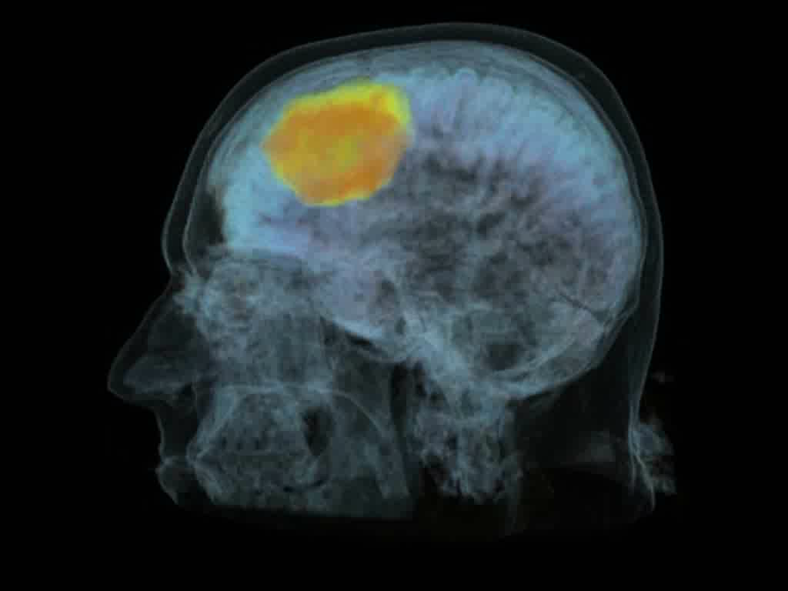
Decision Forests for Semantic Image Segmentation

Decision Forests have been very successful in the space of image segmentation, as a simple, fast and extremely flexible approach well suited to CPU architectures. I developed a framework called BONSAI that cascades small decision forests to allow for semantic reasoning in a more natural manner, for the purpose of structured classification tasks. It also exposes and exploits hidden semantics within decision forests. This is used to implement a form of guided bagging, significantly increasing precision and recall.

Geometry of data, structure, quasi-invariants

Computer science seldom deals with Euclidean data. Data is complex and varies in non linear patterns, but it is also highly structured. It is crucial to leverage and learn this structure, whether to do robust inference from few examples (or one example?) or to best make use of large datasets. Sometimes, structure can also be problem specific, and takes the form of ‘quasi-invariances’ that we wish to enforce in the machine learning. This is a growing interest of mine, and something that I have explored in the context of shape analysis.

Structured Sparse Learning

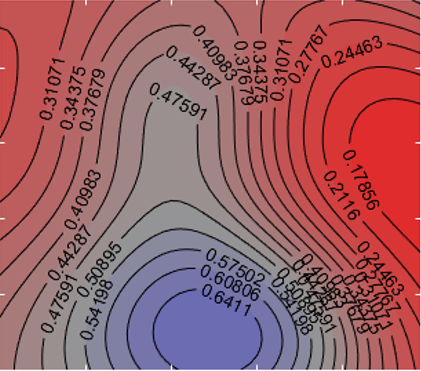
Sparse priors have many uses and motivations – from robust regularization, to reducing the computational complexity of algorithms, to model selection & interpretable machine learning. Sometimes we want to combine the benefits of sparse learning with structured priors that encode a notion of ‘smoothness’ for the problem at hand. This project is about efficient inference schemes for structured sparse learning, in particular with Bayesian priors.

Recent Publications

Contact