We are interested in classification and regression tasks (or in fact, generalized linear models) in which the output variables can be well predicted using a small (but unknown) subset of variables among a large candidate set of explanatory variables (or basis functions). Moreover the predicted variables are known to vary ‘smoothly’ as a function of the input variables. A typical application in medical imaging is to regress activated brain regions in functional MRI. In that case, smooth could be synonymous to ‘contiguous’. As for me, the real-world application was to regress sparse multiscale representations of (physically plausible) displacement fields for medical image registration.
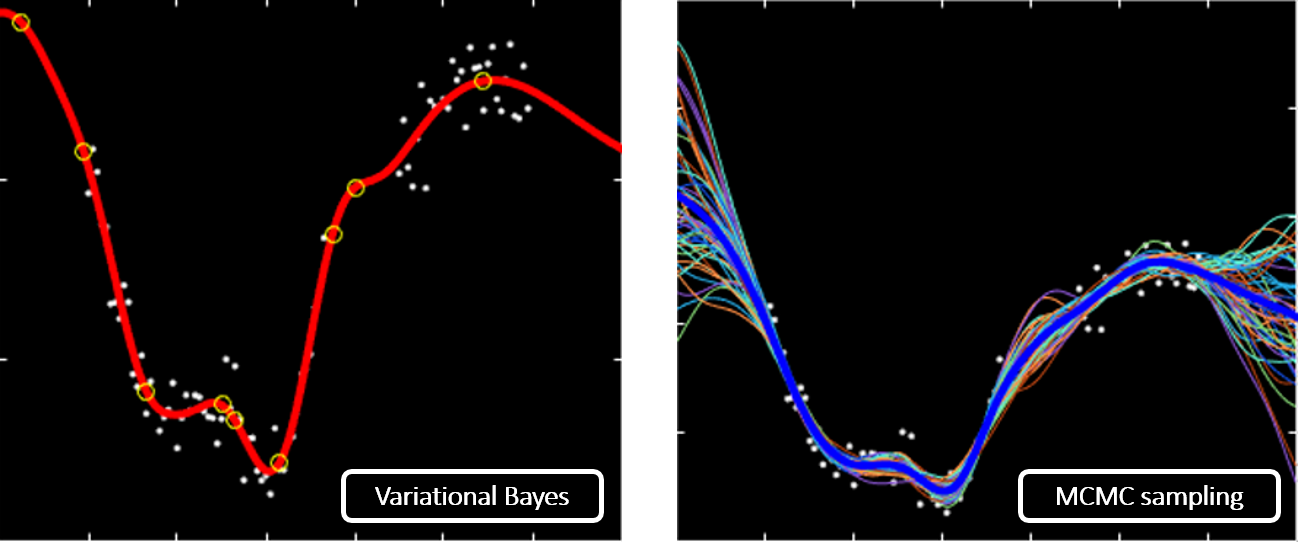
We investigate strongly sparse Bayesian priors that combine a structured Gaussian part (the probabilistic counterpart of Tikhonov regularization) and a point mass whenever a variable is ‘inactive’. The model relates to Spike-&-Slab and to ARD priors. It generalizes Mike Tipping’s sparse Bayesian model of RVM. The RVM (under a specific inference scheme, type-II ML) is also a form of (degenerate) sparse Gaussian process. We pursue two approaches for inference under such models: a generalized variational Bayes (fast) inference scheme (that can be seen as an extension of Tipping’s scheme), and a reversible jump (not as fast?) MCMC approach. Interestingly, the former does tend to give good estimates of the mean but as expected, often inconsistent estimates of uncertainty. We looked into the root causes for such behaviour – it is linked to the choice of variational approximation, which does open future avenues to correct this behaviour within a fast VB inference scheme.